Ejemplo 1.
Después de una prueba de laboratorio muy rigorosa con cierto componente eléctrico, el fabricante determina que en promedio, solo fallarán 2 componentes antes de tener 1 000 horas de operación. Un comprador observa que son 5 los que fallen antes de las 1 000 horas. Si el número de componentes que fallan es una variable aleatoria Poisson ¿Existe suficiente evidencia para dudar de la conclusión del fabricante?
Forma Analítica
En este caso se tiene:
Se supone que la frecuencia con que ocurren las fallas es constante e igual a dos por cada mil horas o un promedio de 1/500 unidades por hora. La probabilidad de que fallen cinco componentes en mil horas es:
Excel
La fórmula que se debe ingresar a excel es: =POISSON(x,media,acumulado), donde el acumulado es un valor lógico que determina la forma de la distribución de probabilidad devuelta. Si el argumento del acumulado es:
- FALSO: la funcón devuelve la probabilidad de Poisson de que un suceso ocurra exactamente x veces.
- VERDADERO: La función devuelve la probabilidad de Poisson de que un suceso aleatorio ocurra un número de veces comprendido entre 0 y x.
Por lo cual la fórmula quedó de la siguiente manera: ‘=POISSON(5,2,FALSE)’.
Ejemplo 2.
Supongamos que el número de accidentes laborales semanales es en promedio 3. Calcular la probabilidad de que en una semana ocurran como mínimo 2 accidentes.
Forma Analítica
Tenemos:
Como resultado final se tiene:
Excel
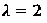





Nos parece muy bueno su blog, viene bien explicado.
ResponderEliminarEn el sengundo ejemplo, el enunciado dice "minimo 2" y en la resolucion se toma en cuenta x=0,1,2. por lo que considera la probabilidad de que no suceda ningun accidente mas la probabilidad de que suceda 1 accidente mas la probabilidad de que ocurran dos accidentes. como si el enunciado dijera maximo 2
ResponderEliminarexacto... tiene que se 1 menos (p(x=0)+p(x=1))
Eliminar