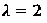viernes, 8 de octubre de 2010
Índice
- Introducción
- Objetivo
- Distribución Poisson
- Ejemplo Poisson
- Solución con R y distr
- Distribución Exponencial
- Ejemplo Exponencial
- Solución con R y distr
- Transformación Poisson-Normal
- Transformación Exponencial-Gamma y Exponencial-Doble Exponencial
- Conclusiones
- Bibliografía
Introducción
El presente trabajo desarrolla de una manera, no muy extensa, las distribuciones poisson y exponencial, aportando un poco de historia para cada una de las distribuciones, con el fin de complementar el objetivo de dicha investigación, así como para dar a conocer otros aspectos, que consideramos importantes mencionar para dichas distribuciones, ya que en la gran mayoría de trabajos se omite este tipo de información.
Objetivo
El objetivo de ésta investigación que se llevó a cabo sobre las distribuciones poisson y exponencial, radica en analizar las características de cada una de dichas distribuciones de forma sintética, de tal manera que el lector pueda entender con sencillez, la aplicación de cada una de éstas distribuciones, ayudándonos de dos ejemplos prácticos resueltos de manera analítica, en Excel y en R para cada uno de los temas aquí expuestos.
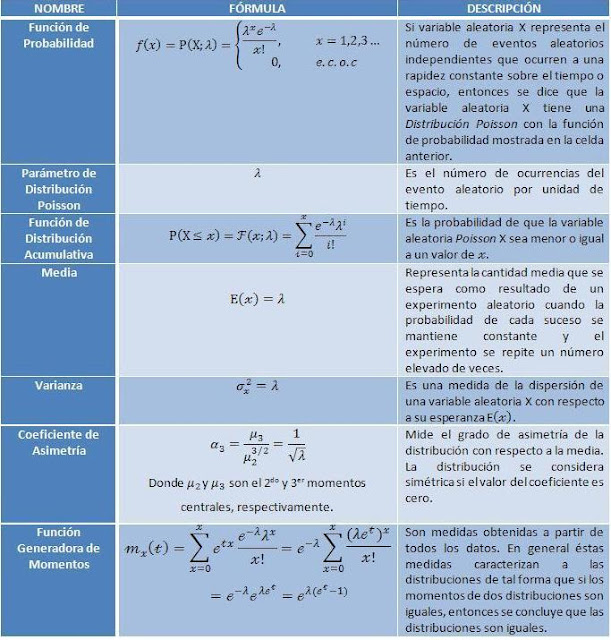
Distribución Poisson
Es llamada así en honor a Simeón Denis Poisson (1781-1840), quién fue el primero en describirla en 1838 en su trabajo Recherches sur la Probabilité des Jugements en matiéres criminelles et matiére civile, y que es aplicable a fenómenos poco comunes o extraños.
La Distribución Poisson es una distribución de probabilidad discreta muy útil en la que la variable aleatoria representa el número de eventos independientes que ocurren a una velocidad constante. La Distribución de Poisson es el principal modelo de probabilidad empleado para analizar problemas de línea de espera. También ofrece una aproximación excelente a la Función de Probabilidad Binomial cuando p es pequeño y n es grande.
La convergencia de la función de probabilidad Binomial hacia la Poisson tiene un valor práctico, porque se pueden utilizar las probabilidades de Poisson para aproximar sus correspondientes binomiales para valores valores grandes de n, valores pequeños de p, y lambda=np menor que 7.
La Distribución de Poisson proporciona muchas veces un muy buen modelo para la distribución de probabilidad para el número Y de eventos raros que ocurren infrecuentemente en el espacio, tiempo, volúmen o cualquier otra dimensión, en donde
La convergencia de la función de probabilidad Binomial hacia la Poisson tiene un valor práctico, porque se pueden utilizar las probabilidades de Poisson para aproximar sus correspondientes binomiales para valores valores grandes de n, valores pequeños de p, y lambda=np menor que 7.
La Distribución de Poisson proporciona muchas veces un muy buen modelo para la distribución de probabilidad para el número Y de eventos raros que ocurren infrecuentemente en el espacio, tiempo, volúmen o cualquier otra dimensión, en donde
representa el valor promedio de y. Es decir, proporciona un buen modelo para la distribución de probabilidad del número Y de:
- accidentes automovilísticos
- accidentes industriales
u otro tipo de accidentes en la unidad de tiempo dada.
Cuando el número de resultados dados en un intervalo continuo son contados, una aproximación de la Distribución de Poisson con parámetro:
resulta si se satisfacen las condiciones siguientes:
1) El número de resultados en el intervalo de tiempo (0,t] son independientes del número de resultados en el intervalo de tiempo (t,t+h] para cualquier h>0.
2) La probabilidad de dos o más resultados en un intervalo suficientemente corto es prácticamente cero. En otras palabras, h siempre es suficientemente pequeña, la probabilidad de obtener dos o más resultados en el intervalo (t,t+h] es insignificante en comparación a la probabilidad de obtener uno o cero resultados en el mismo intervalo de tiempo.
3) La probabilidad de que exactamente uno de los resultados en un intervalo suficientemente corto o una región pequeña es proporcional a la longitud del intervalo o región. En otras palabras, la probabilidad de un resultado en un intervalo de longitud h es:
Ejemplo Poisson
Ejemplo 1.
Después de una prueba de laboratorio muy rigorosa con cierto componente eléctrico, el fabricante determina que en promedio, solo fallarán 2 componentes antes de tener 1 000 horas de operación. Un comprador observa que son 5 los que fallen antes de las 1 000 horas. Si el número de componentes que fallan es una variable aleatoria Poisson ¿Existe suficiente evidencia para dudar de la conclusión del fabricante?
Forma Analítica
En este caso se tiene:
Se supone que la frecuencia con que ocurren las fallas es constante e igual a dos por cada mil horas o un promedio de 1/500 unidades por hora. La probabilidad de que fallen cinco componentes en mil horas es:
Excel
La fórmula que se debe ingresar a excel es: =POISSON(x,media,acumulado), donde el acumulado es un valor lógico que determina la forma de la distribución de probabilidad devuelta. Si el argumento del acumulado es:
- FALSO: la funcón devuelve la probabilidad de Poisson de que un suceso ocurra exactamente x veces.
- VERDADERO: La función devuelve la probabilidad de Poisson de que un suceso aleatorio ocurra un número de veces comprendido entre 0 y x.
Por lo cual la fórmula quedó de la siguiente manera: ‘=POISSON(5,2,FALSE)’.
Ejemplo 2.
Supongamos que el número de accidentes laborales semanales es en promedio 3. Calcular la probabilidad de que en una semana ocurran como mínimo 2 accidentes.
Forma Analítica
Tenemos:
Como resultado final se tiene:
Excel
Solución con R y distr (Poisson)
En R utilizamos la función:
Descarga el archivo en WORD
dpois( x , lambda , FALSE O TRUE)
Con parámetros:
x:= probabilidad
λ= promedio o media
Valor lógico= Si es TRUE las probabilidades se dan como log(p)
- Ejemplo 1 (Componentes Eléctricos)
En R utilizamos la función dpois que tiene el siguiente formato:
dpois(x,lambda,long=FALSE)
Sustituyendo los valores queda de la siguiente manera:
- Ejemplo 2.(Accidentes Laborales)
En este caso añadimos otra función que nos haga la suma de las probabilidades
de poisson [P(0)+P(1)+P(2)] y es sum(). Por lo tanto queda de la siguiente manera:
En distr Declaramos un objeto:
- Ejemplo 2. (Accidentes Laborales)
Distribución Exponencial
Ésta distribución es un caso especial de la distribución gamma, la variable aleatoria exponencial es el tiempo que transcurre hasta que se da el primer evento de Poisson. Es decir, la distribución exponencial puede modelar el lapso entre dos eventos consecutivos de Poisson que ocurren de manera independiente y a una frecuencia constante.
Describe procesos en los que interesa saber el tiempo hasta que ocurre un determinado evento, sabiendo que el tiempo que puede transcurrir desde cualquier instante dado t, hasta que ello ocurra en un instante tf, no depende del tiempo transcurrido anteriormente.
Ejemplos Exponencial
Ejemplo 1.
En una carretera el número de autos que excede el límite de velocidad en más de 10 millas por hora es una variable aleatoria que tiene una distribución Poisson con λ =8.4. ¿Cuál es la probabilidad de un tiempo de espera menor de 5 minutos entre autos que excede el límite de velocidad en más de 10 millas por hora?
Entonces la probabilidad de un tiempo de espera menor de 5 minutos entre autos que exceden la velocidad máxima es de 0.75.
Descarga el archivo en WORD
En una carretera el número de autos que excede el límite de velocidad en más de 10 millas por hora es una variable aleatoria que tiene una distribución Poisson con λ =8.4. ¿Cuál es la probabilidad de un tiempo de espera menor de 5 minutos entre autos que excede el límite de velocidad en más de 10 millas por hora?
Esto es …
Así tenemos:
Entonces la probabilidad de un tiempo de espera menor de 5 minutos entre autos que exceden la velocidad máxima es de 0.75.
Ejemplo 2.
Se ha comprobado que el tiempo de vida de un marcapasos es en promedio 16 años. ¿Cuál es la probabilidad de que una persona a la que se le ha implantado este marcapasos se le deba reimplantar otro antes de 20 años?
Entonces la probabilidad de que a una persona se le reimplante un marcapasos antes de 20 años es de 0.7175.
Solución con R y distr (Exponencial)
Utilizamos la función del paquete stats en R:
Descarga el archivo en WORD
pexp( x , rate , lower.tail )
Parámetros:
x:= probabilidad
rate:= tasa de cambio 1/ λ
lower.tail:= Si es TRUE entonces P[X≤ x]de lo contrario P[X≥ x].
- Ejemplo 1. (Autos que exceden el límite de velocidad)
- Ejemplo 2.(Tiempo de vida de un marcapasos)
Exp( tasa = media)
- Ejemplo 1. (Autos que exceden el límite de velocidad)
- Ejemplo 2. (Tiempo de vida de un marcapasos)
Transformación Poisson-Normal
Aproximación Normal a Probabilidades Poisson.
Una distribución Poisson con parámetro λ se aproxima a la Normal para grandes valores de λ.
Donde λ MUY GRANDE .
Parámetros de Poisson
μ =σ = λ
Parámetros en la Normal
Del ejemplo 2 (Animales vagabundos muertos)
Para x= 1
Checando tablas dse obtiene:
Transformación Exponencial-Gamma y Exponencial-Doble Exponencial
Exponencial resuelta por la distribución Gamma
Ejemplo 2.
Se ha comprobado que el tiempo de vida de un marcapasos es en promedio 16 años. ¿Cuál es la probabilidad de que una persona a la que se le ha implantado este marcapasos se le deba reimplantar otro antes de 20 años?
En una distribución gamma:
Doble Exponencial
La distribución Doble Exponencial también es conocida como Distribución de Laplace.
Es la diferencia de dos variables exponenciales aleatorias, independientes e idénticamente distribuidas.
Función de densidad:
Parámetros:= μ =parámetro de localización b= parámetro de escala
Media = μ Varianza = 2 (b ^2)
Descarga el archivo en WORD
viernes, 1 de octubre de 2010
Conclusiones
Tanto la distribución Poisson como la Exponencial tienen diversas aplicaciones en la vida real, las cuales tienen relación una con otra, y no sólo eso, sino que hay otras distribuciones que tienen relación con las antes mencionadas y es por eso que tiene su importancia conocerlas.
Podemos decir, entonces, algunos ejemplos prácticos de las dos distribuciones:
- La distribución Poisson se utiliza para calcular la probabilidad del número de llamadas telefónicas manejadas por un conmutador en un intervalo, el número de partículas radiactivas que decaen en un periodo particular y el número de errores que comete una secretaria al mecanografiar una página.
- La distribución Exponencial se utiliza para estudios de confiabilidad y es utilizado por describir el crecimiento bacteriológico y el interés compuesto.
A pesar de que solo se dieron dos ejemplos para cada una de las distribuciones, creemos que fué importante porque no solo se resolvieron de forma analítica, sino que se usó Excel y R que es un software estadístico de mucha ayuda para resolver problemas de este tipo y otros tantos más.
Bibliografia
- Canavos, C. George, “Probabilidad y Estadística, Aplicaciones y Métodos", 1988, McGraw-Hill.
- Mendenhall, William."Estadística Matemática con Aplicaciones", 1986,Grupo Editorial Iberoamércia.
- Murray R. Spiegel, “Probabilidad y Estadística, Teoria y 760 problemas resueltos”, 1976, McGraw-Hill.
- Ugarte, María Dolores, “Probability and Statistics With R”, 2008, CRC Press.
Cibergrafía
- http://web.frm.utn.edu.ar/estadistica/_AutoevaluacionesPDF/VFCapitulo_06.PDF Fecha : 25/09/2010 hora: 7:37 p.m.
- http://books.google.com/books?id=nDcKrcCAOo8C&pg=PA143&dq=probabilidad+discreta&lr=&hl=es&cd=29#v=onepage&q=probabilidad%20discreta&f=false Fecha: 26/09/2010 hora: 3:32 p.m.
- www1.uprh.edu/.../La%20distribucion%20Poisson/Modulo%20Sobre%20La%20Distribucion%20de%20Poissonl%20 Fecha: 26/09/2010 hora: 8:45p.m.
Suscribirse a:
Comentarios (Atom)